Guide for Using Composite Indexes and Diffusion Indexes
The indexes of business conditions are summary measures for aggregate economic activity. They are designed to be a useful tool for analyzing current conditions, and for forecasting future economic conditions. They are indexes that combine the behavior of key cyclical indicators that represent widely differing activities of the economy such as production, employment, and many more.
The composite indexes are used to identify the volume of overall business activities by composing percentage changes of selected indicators. On the other hand, diffusion indexes are used to measure the degree of propagation of economic expansion, among other purposes, by counting the number of indicators with the same direction of changes.
1. Overview: How to Use the Composite Indexes
(Objective)
The composite indexes mainly aim to measure the tempo and the magnitude ("the volume") of economic fluctuations. They compose the quantitative changes in indicators that are sensitive to business cycle movements.
(Using composite indexes)
There are three types of composite indexes:
1) The leading CI
This tends to precede the coincident CI by a few months, and is used to anticipate changes in the direction of the economy.
2) The coincident CI
This coincides with the business cycle, and is used to identify the current state of the economy.
3) The lagging CI
This tends to lag behind the coincident CI by about six months, and is used to confirm turning points and business cycle phases.
In general, increasing the coincident index reflects that the economy is in an expansion phase, and decreasing coincident index reflects that the economy is in a contraction phase. The magnitude of the changes in the coincident index reflects the tempo of the expansion or contraction phases. However, not only the composite indexes but also the diffusion indexes should be considered in order to identify whether the economy is in an expansion or contraction phase, or to date business cycle turning points, the details of which are described below. Furthermore, it should be noted that, because the composite indexes are the summary measures of quantitative movement of component indicators selected for their sensitivity to business cycles, they do not necessarily cover the full range of economic activities. Currently, the composite indexes use the same selected series of indicators as the diffusion indexes, i.e. 30 series of indicators in total: 11 leading indicators, 10 coincident indicators, and 9 lagging indicators. The list of selected series of indicators is reviewed each time the economy goes through a peak or a trough. We began operation with the current 30 series since the preliminary release for January 2021 according to the schedule decided on the Committee Business Cycle Indicators (July 30, 2020).
(1 series (Index of Shipment in Small and Medium Sized Enterprises (Manufacturing)) of components (Coincident Index) has been excluded (March 8, 2017), because the updating of "Indices of Industrial Production on SMEs" was ceased in February, 2017.)
An increase or decrease of the composite indexes for an extremely short period of time should not be interpreted as a sign of economic expansion or contraction. Moreover, the composite indexes must move up or down with a certain magnitude in order to interpret that the economy has taken an upward or downward turn.
When analyzing month-to-month movements of the composite indexes, it is advisable to smooth out idiosyncratic fluctuations using a moving average, although the outliers of the individual indicators are truncated to eliminate the effects of them to the changes in the composite indexes. The three-month backward moving average, which is useful to monitor short-term tendencies, as well as the seven-month backward moving average, which is useful for confirming that the cyclical changes, should be considered for the assessment of the coincident CI.
(Differences from the diffusion indexes)
The diffusion indexes are used to measure the degree of propagation of economic expansions. They measure the proportion of the component indicators that are improving. When the diffusion indexes are above the threshold value of 50 percent, the economy can be interpreted to be in an expansion phase; when below, in a contraction phase.
On the other hand, the composite indexes provide a quantitative measurement of economic strength. The composite indexes differentiate between small and large overall movements. They are referred to as the indexes that indicate the "volume" of economic activities, e.g. the amplitude of economic peaks and troughs, as well as the speed of economic expansion or contraction. For a better comparison of changes in different economic perspectives, it is recommended to use both the contributions of the component series to the change in the composite indexes and the diffusion indexes.
(Calculating the composite indexes)
The composite indexes are calculated by composing month-to-month percentage changes in multiple economic indicators. As a simplified example, assume that one of the composite indexes is constructed from two indicators, Indicator A and Indicator B ("y1" and "y2" in the figure below). In a certain month, Indicators A and B are higher than the previous month by 1 percent and 0.5 percent respectively ("γ1" and "γ2" in the same figure). These change rates are averaged, and the average is multiplied by the previous month's level of the composite index to obtain the current month's level.
The change rates with different volatilities are subjected to a process called "normalization" before averaging so that they can be evaluated on a common basis. Assume a situation in which Indicator A shows an upward trend and large monthly fluctuations, while Indicator B shows a flat trend and small monthly fluctuations. In this situation, the change rates have different meanings between Indicator A and B.
The normalization process is performed taking into consideration two types of elements: trend and amplitude. Assume that Indicator A has a trend of 2 percent and an amplitude of 0.5 percent, the normalized percentage change rate for Indicators A is calculated as follows:
(Change rate for the current month 1 - Trend 2) / (Amplitude 0.5) = -2.
Similarly, assume that Indicator B has a trend of 0 percent and an amplitude of 0.2 percent, the normalized percentage change rate for Indicator B is calculated as follows:
(Change rate for the current month 0.5 - Trend 0) / (Amplitude 0.2) =2.5.
Then, the "composite normalized percentage change rate," Z, is calculated as follows, by averaging the normalized percentage change rates of Indicators A and B:
Z = (-2 + 2.5) / 2 = 0.25.
Because Z is an average of "normalized" variables, it should be inversely transformed to recover amplitude and trend. The following two steps take place: (1) the composite normalized percentage change Z is multiplied by the composite amplitude σ, which is obtained by averaging the amplitudes of Indicator A and B; and (2) the composite trend μ is added to the result of step (1). The result of the two steps represents the composite "month to month percentage change" V. Then, the current month's composite index is obtained by multiplying V by the previous month's level of the composite index. Individual indicators' month-to-month percent change rate is calculated using a "symmetric percentage change." The symmetric percentage change uses for the denominator an average of the previous and current month values (mean value), instead of the previous month's level, as in the ordinary calculation of month-to-month ratios. When calculating the composite index based on V, the symmetric percentage change formula is used inversely.
Composite index calculation flow and examples of values (when the composite index is constructed from two indicators)
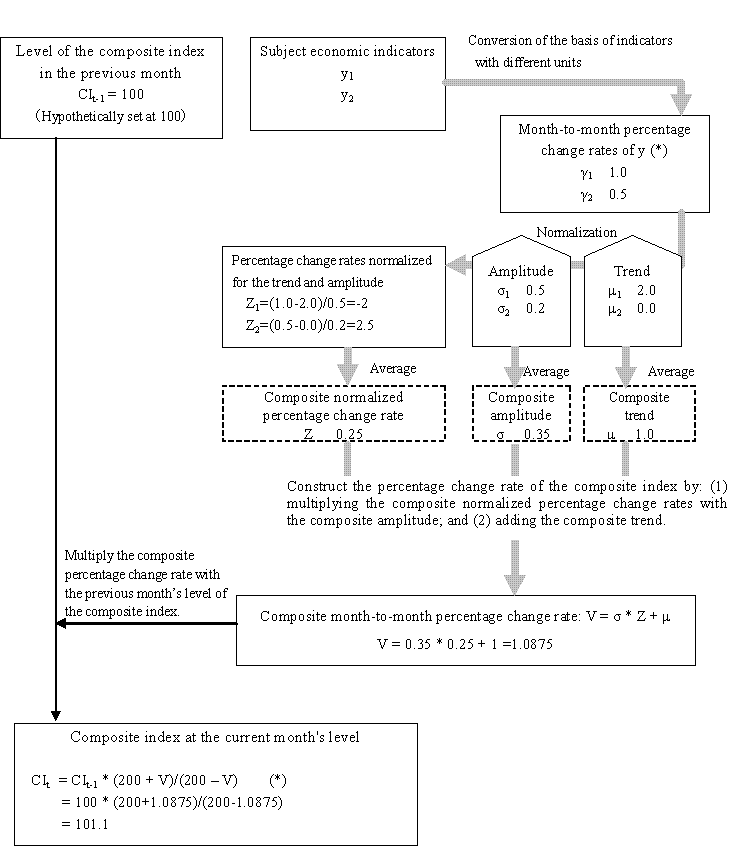
The “symmetric percentage change” is used in the calculation of the month-to-month percentage change rate γ, as well as in the calculation of the composite index inversely from V with the formula marked with ( *) .
The symmetric percentage change uses the average of previous and current months as denominator:γt=(уt‐уt-1)/((уt+уt-1)/2*100.
2. The calculation method
The calculation method is as follows.
Step 1: The previous formula is used for calculating the symmetric percent change (![]() ) of individual series (
) of individual series (![]() ), as in the following. In the notation below, i subscript refers to the number assigned to each indicator.
), as in the following. In the notation below, i subscript refers to the number assigned to each indicator.
![]()
If the given time series is zero or a negative value, or is already in percentage form, simple arithmetic differences are calculated.
![]()
Then, outliers (found only in the specific movement of each indicator as below) are replaced using the following step.
Step 1-1: The trend of individual series (mean percent change![]() ) is calculated by the 60-month backward moving average.
) is calculated by the 60-month backward moving average.
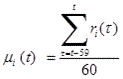
Step 1-2: Percent change normalized by interquartile range (![]() ) is calculated by applying the following formula.
) is calculated by applying the following formula.
![]()
![]() is the first quartile in the interquartile range and
is the first quartile in the interquartile range and ![]() is the third quartile in the interquartile range of the symmetric percent change (
is the third quartile in the interquartile range of the symmetric percent change (![]() ).
).
Step 1-3: Median of percent change normalized by interquartile range (![]() ) is chosen for the common cyclical movement (
) is chosen for the common cyclical movement (![]() ).
).
![]()
Step 1-4: The specific movement of each indicator (![]() ) is calculated by subtracting the common cyclical movement from percent change normalized by interquartile range.
) is calculated by subtracting the common cyclical movement from percent change normalized by interquartile range.
![]()
Step 1-5: The symmetric percent change for the specific movement of each indicator (![]() ) is calculated by adding up trend and the specific movement of each indicator multiplied by interquartile range.
) is calculated by adding up trend and the specific movement of each indicator multiplied by interquartile range.
![]()
Step 1-6: The symmetric percent change for the common cyclical movement (![]() ) is calculated by multiplying the common cyclical movement by interquartile range.
) is calculated by multiplying the common cyclical movement by interquartile range.
![]()
Step 1-7: Outliers in the symmetric percent change for the specific movement of each indicator (![]() ) are replaced using the following formula.
) are replaced using the following formula.
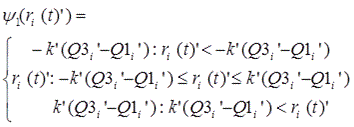
![]() is the first quartile in the interquartile range and
is the first quartile in the interquartile range and ![]() is the third quartile in the interquartile range of the symmetric percent change for the specific movement of each indicator (
is the third quartile in the interquartile range of the symmetric percent change for the specific movement of each indicator (![]() ).
).
Then, the symmetric percent change for the common cyclical movement is added.
![]()
Step 2: Again, the trend of individual series (mean percent change![]() ) is calculated by the replaced 60-month backward moving average.
) is calculated by the replaced 60-month backward moving average.
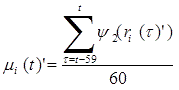
Percent change normalized by interquartile range (![]() ) is calculated by applying the following formula.
) is calculated by applying the following formula.
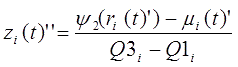
Step 3: Composite percentage change (![]() ) is calculated by adding up trend (composite mean percent change,
) is calculated by adding up trend (composite mean percent change,![]() ) and the mean of percent change normalized by interquartile range (composite percent change normalized by interquartile range,
) and the mean of percent change normalized by interquartile range (composite percent change normalized by interquartile range,![]() ). In this process, composite percent change normalized by interquartile range is multiplied by the mean of interquartile ranges (composite interquartile range,
). In this process, composite percent change normalized by interquartile range is multiplied by the mean of interquartile ranges (composite interquartile range,![]() ) so that the levels of the trend component and the cyclical component coincide.
) so that the levels of the trend component and the cyclical component coincide.
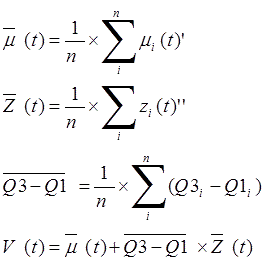
where n represents the number of indicators.
Step 4:Composite percentage change is cumulated. Finally, the index is rebased so that the value for the reference year is 100.
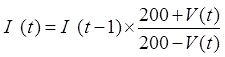
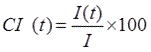 (
(![]() is the average of the reference year
is the average of the reference year![]() )
)
Notes for calculation
- For calculating the leading composite index and the lagging composite index, the trend component of coincident composite index is applied as in the previous method.
- The threshold for Winsorized value, k', by which 5 percent of the data in the coincident series from the January 1985 to the latest December are regarded as outliers.
- With regard to dealing with missing data of indicators because of late publication in calculating composite indexes, the trend is calculated by using the available data of all the indicators at that time. For example, if an indicator has data for only 57 months, then the 57- month data are used in calculating the trend. On the other hand, when calculating composite percentage change normalized by interquartile range, indicators with missing data are excluded. As a result, the latest composite percent change normalized by interquartile range does not include all of the indicators.
Reference: Yoshizoe et al., "Expansion of Traditional Indicators," in "New Developments in Business Cycle Indicators," Economic Analysis, No. 166, December 2001, Economic and Social Research Institute, Cabinet Office.
3. The Reference Dates of Business Cycle
The reference date of a business cycle is first discussed in the Committee for Business Cycle Indicators, based on historical diffusion index, which is composed of the same selected series as coincident composite indexes. Based on the discussion, the President of ESRI determines the reference date. In the historical diffusion index, first the peaks and troughs for each selected time series of composite indexes are determined (this is referred to as the individual turning point). The historical diffusion index is defined as the fraction of expanding series, i.e., series climbing from a trough to the next peak. Since the change in direction is determined by smoothing irregular month-to-month movements of individual time series, the historical diffusion index calculated from these values is relatively smooth, and reflects the basic movement of the business cycle. Along the way of fluctuation of it, the last month when the historical diffusion index compiled from a selected series of coincident indexes stays below the 50-percent line corresponds to the cyclical trough; the last month when this index stays above the 50-percent line corresponds to the cyclical peak.
In addition, the peaks and troughs of each individual time series is dated by applying the Bry-Boschan method, which was developed by the U.S. National Bureau of Economic Research (NBER). This method determines the cyclical peak or trough by providing a series of rules. Two examples of this rule: that five months or more are required in the period between peak and trough, and that the duration of one cycle must be 15 months or more. This procedure, which also involves handling of several types of moving average, was presented along with a computer program to actually run it.
Reference: Bry & Boschan (1971) Cyclical Analysis of Time Series: Selected Procedures and Computer Programs, NBER, New York.
| Trough | Peak | Trough | Duration | (Reference) Dated by quarters |
|||
|---|---|---|---|---|---|---|---|
| Expansion | Contraction | Entire cycle | Peak | Trough | |||
| Jun.1951 | Oct.1951 | 4 months | 2Q 1951 | 4Q 1951 | |||
| Oct.1951 | Jan.1954 | Nov.1954 | 27 months | 10 months | 37 months | 1Q 1954 | 4Q 1954 |
| Nov.1954 | Jun.1957 | Jun.1958 | 31 months | 12 months | 43 months | 2Q 1957 | 2Q 1958 |
| Jun.1958 | Dec.1961 | Oct.1962 | 42 months | 10 months | 52 months | 4Q 1961 | 4Q 1962 |
| Oct.1962 | Oct.1964 | Oct.1965 | 24 months | 12 months | 36 months | 4Q 1964 | 4Q 1965 |
| Oct.1965 | Jul.1970 | Dec.1971 | 57 months | 17 months | 74 months | 3Q 1970 | 4Q 1971 |
| Dec.1971 | Nov.1973 | Mar.1975 | 23 months | 16 months | 39 months | 4Q 1973 | 1Q 1975 |
| Mar.1975 | Jan.1977 | Oct.1977 | 22 months | 9 months | 31 months | 1Q 1977 | 4Q 1977 |
| Oct.1977 | Feb.1980 | Feb.1983 | 28 months | 36 months | 64 months | 1Q 1980 | 1Q 1983 |
| Feb.1983 | Jun.1985 | Nov.1986 | 28 months | 17 months | 45 months | 2Q 1985 | 4Q 1986 |
| Nov.1986 | Feb.1991 | Oct.1993 | 51 months | 32 months | 83 months | 1Q 1991 | 4Q 1993 |
| Oct.1993 | May 1997 | Jan.1999 | 43 months | 20 months | 63 months | 2Q 1997 | 1Q 1999 |
| Jan.1999 | Nov.2000 | Jan.2002 | 22 months | 14 months | 36 months | 4Q 2000 | 1Q 2002 |
| Jan.2002 | Feb.2008 | Mar.2009 | 73 months | 13 months | 86 months | 1Q 2008 | 1Q 2009 |
| Mar.2009 | Mar.2012 | Nov.2012 | 36 months | 8 months | 44 months | 1Q 2012 | 4Q 2012 |
| Nov.2012 | Oct.2018 | May 2020 | 71 months | 19 months | 90 months | 4Q 2018 | 2Q 2020 |
